备课教案
|
教学内容
| 第五单元 三角形
|
课时
| 课时四:三角形的内角和
|
主备人
| 数学教研组
| 所在学校
| |
教材分析
| 教材先通过学生度量不同的三角形的内角和,感知他们的和是180度,再通过实验的方法去验证。
|
教学目标
| 知识目标
| 认识三角形的内角和是180度这一特性;
|
| 能力目标
| 运用三角形的内角和根据已知角的度数求未知角的度数;
|
| 情感目标
| 通过引导学生自主探索、动手操作、培养初步的创新精神和实践能力。
|
教学重点
| 认识三角形的内角和是180度这一特性;
|
教学难点
| 运用三角形的内角和根据已知角的度数求未知角的度数;
|
教学准备
| 三角形纸板、教学课件
|
教 学 过 程
|
教 学 内 容
| 学生活动
| 补充、 总结
|
一、复习准备
1.三角形按角的不同可以分成哪几类?
2.一个平角是多少度?1个平角等于几个直角?
3.三角形按角的不同可以分成哪几类?
二、教学新课
1.三角形有几个角?老师指出:三角形的这三个角,就叫做三角形的三个内角。
2.三角形三个内角的度数和叫做三角形的内角和。(板书课题:三角形的内角和)今天我们一起来研究三角形的内角和有什么规律。
3.以小组为单位利用手中的工具分别测量计算三角形三个内角的和各是多少度?
4.指名学生汇报各组度量和计算的结果。你有什么发现?
5.大家算出的三角形的内角和都接近180°,那么,三角形的内角和与180°究竟是怎样的关系呢?就让我们一起来动手实验研究,我们一定能弄清这个问题的。
6.刚才我们计算三角形的内角和都是先测量每个角的度数再相加的。在量每个内角度数时只要有一点误差,内角和就有误差了。我们能不能换一种方法,减少度量的次数呢?
提示学生,可以把三个内角拼成一个角,就只需测量一次了。
7.请拿出桌上的直角三角形纸片,想一想,怎样折可以把三个角拼在一起,试一试。
8.三个角拼在一起组成了一个什么角?我们可以得出什么结论?(直角三角形的内角和是180°)
9.拿一个锐角三角形纸片试试看,折的方法一样。再拿钝角三角形折折看,你发现了什么?(直角三角形和钝角三角形的内角和也是180°)。
如图:
<Object: word/embeddings/oleObject1.bin>
10.那么,我们能不能说所有三角形的内角和都是180°呢?为什么?(能,因为这三种三角形就包括了所有三角形)
11.老师板书结论:三角形的内角和是180°。
12.一个三角形中如果知道了两个内角的度数,你能求出另一个角是多少度吗?怎样求?
13.出示教材85页做一做。让学生试做。
14.指名汇报怎样列式计算的。两种方法均可。
∠2=180°-140°-25°=15°
∠2=180°(140°+25°)=15°
三、巩固练习
1.69页第1题
这一题是不是只知道一个角的度数?另一个角是多少度,从哪看出来的?独立完成,集体订正。
直角三角形中的一个锐角还可以怎样算?
四、布置作业
69页第2、4题
五、板书设计
三角形的内角和
<Object: word/embeddings/oleObject2.bin>
三个角拼在一起组成了一个什么角?我们可以得出什么结论?
三角形的内角和是180°
∠2=180°-140°-25°=15°
∠2=180°(140°+25°)=15
1、有一个三角形,其中一个角是20°,它可能是什么三角形?如果还知道第二个角是65°,那么你知道它是什么三角形了吗?
2.在一个直角三角形中,已知一个锐角是35°,另一个锐角是多少度?
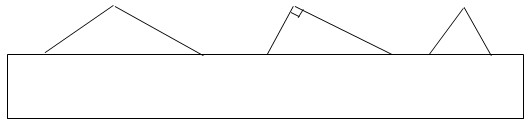
3.下面的三角形都被一张纸遮住了一部分。你能确定它们各是什么三角形吗?
| 请学生回答
教师板书内角和
小组测量计算
三角形三个内角的和,汇报,
学生把三个角拼在一起
学生完成,教师指导
| |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
![]() 川公网安备51152402000101号 )|网站地图
川公网安备51152402000101号 )|网站地图